Question 6:
Read the given question and decide which of the information is sufficient to answer the question?
What is the value of $\angle A C D$
Information:
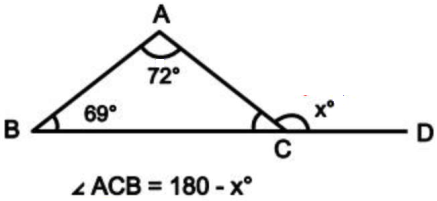
दिए हुए प्रश्न को पढ़ें और तय करें कि कौन सी सूचना प्रश्न का उत्तर देने के लिए पर्याप्त है?
$\angle \mathrm{ACD}$ का मान कितना है?
सूचना:


